摘要
本篇文章笔记总结来自网络和书本,引用部分都有来源,内容主要介绍隐马尔科夫HMM相关实际应用搞得入门例子,很简单,但是能说明隐马尔科夫HMM的原理相关。
- [x] Edit By Porter, 积水成渊,蛟龙生焉。
文章同步于: 我的gitbook
HMM(隐马尔可夫模型)
隐马尔可夫模型是一种统计模型,用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析,例如模式识别。
是在被建模的系统被认为是一个马尔可夫过程与未观测到的(隐藏的)的状态的统计马尔可夫模型。
本文简述的是离散情况下的隐马尔可夫模型.
一、贝叶斯公式
定义:假设以硬币的例子,从5角和1元的一堆硬币中,随意取出一枚硬币,然后然我们猜这枚硬币是5角还是1元。假设允许我们称这枚硬币的重量x(单位:g),(但是不允许我们直接看硬币,一般1元是比5角重的)。现在应考察在一直这枚硬币的重量x的情况下硬币属于各类(5角还是一元)的概率,分别记$$P(\omega_{1}|x)$$,(知重量为x时,是5角的概率),$$P(\omega_{2}|x)$$, (知重量为x时,是一元的概率),这种概率成为后验概率(我们需要求的)。这时的决策为:如果$$P(\omega_{1}|x)>P(\omega_{2}|x)$$,则$$x \epsilon \omega_{1} $$; 反之,则$$x \epsilon \omega_{2} $$
- 最终我们要的就是这个决策。
概率论中的贝叶斯公式:
| 分布 | 表示 | $$x \epsilon \left { \omega_{1},\omega_{2} \right }$$ |
|---|---|---|
| 类条件概率: | $$p(x\mid \omega_{i})$$ | 表示得到硬币结果是$$\omega_{i}$$条件下,得到x的概率密度 |
| 后验概率: | $$P(\omega_{i}\mid x)$$ | 在重量为x,的条件下,得到是哪种硬币(5/1)的概率 |
| 先验概率: | $$P(\omega_{i})$$ | 根据之前的经验,得到5角和1元各自取得的概率 |
| 硬币重量概率密度函数: | $$p(x)$$ | 硬币重量的概率密度函数 |
| 联合概率密度: | $$p(x,\omega_{i})$$ | 在重量不同条件下,每种情况对应的取得不同硬币结果的联合概率 |
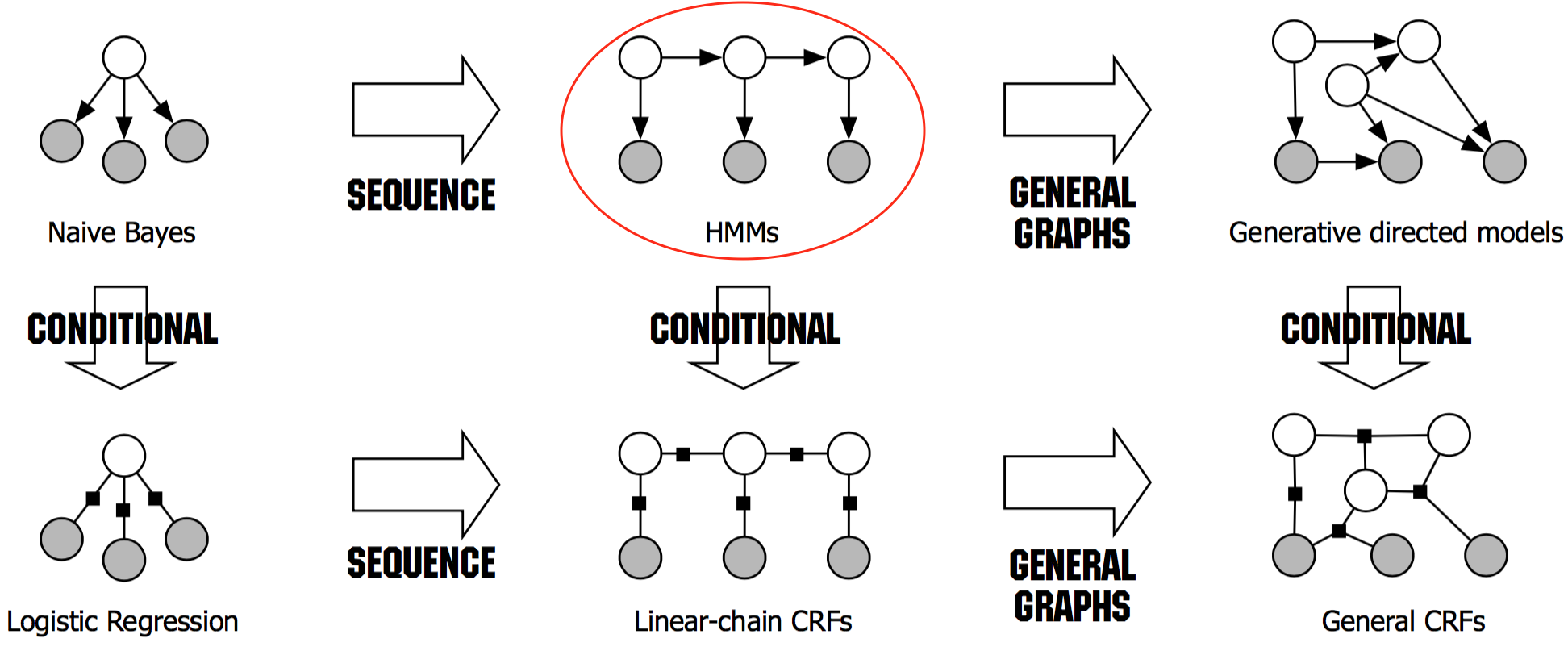
P(Q_{i}|O)$$ ,后验概率,$$P(O,Q_{i})$$ ,表示O与Q的联合概率密度;P(O)表示两类所有的概率密度; P(Q_{i})是先验概率;$$P(O|Q_{i})$$是第i类状态随机序列的类条件概率密度 > 贝叶斯决策:在类条件概率密度和鲜艳概率已知(或可估计)的情况下,通过贝叶斯公式比较样本属于两类的后验概率,将类别决策为后验概率大的一类,这样做的目的是为了使总体错误率最小。 一条隐藏的马尔可夫链生成的 **状态随机序列** (State sequence, 图中的白色节点) $$Q=(q_{1},q_{2},.....,q_{T})$$是**不可观测的**,并记所有可能状态的集合为$$S={S_{1},S_{2},.....,S_{N}}$$;由它们产生一个**可观测的观测随机序列**(observation sequence,图示的深色节点)$$O=(o_{1},o_{2},......,o_{T})$$, 并记所有可能观测的集合为$$V={v_{1},v_{2},......,v_{M}}$$。 序列的值可以看作是随时刻产生的,每个时刻对应着序列的一个值。所以HMM是个双重随机过程(doubly embedded stochastic process),一个是状态转移,另一个是由状态释放出观测值。在序列标注(Sequence labelling)任务中,模型就是需要对状态序列进行标注。