本篇文章笔记总结来自网络和书本,引用部分都有来源,内容主要介绍线性回归相关基础相关实际应用搞得入门例子,很简单,但是能说明线性回归相关基础的原理相关。
[x] Edit By Porter, 积水成渊,蛟龙生焉。 文章同步于: 我的gitbook
学习参考来源
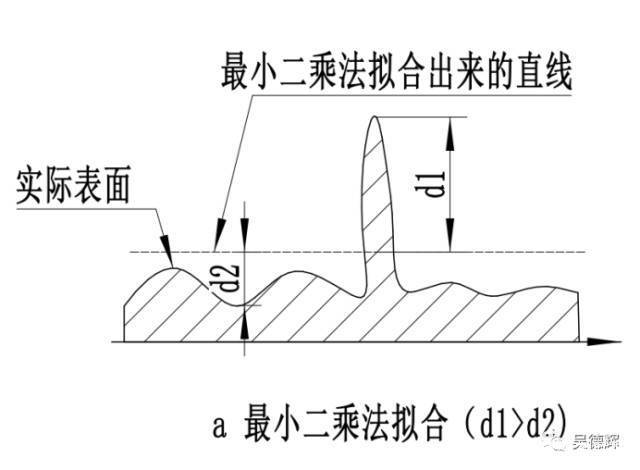
最小二乘法定义如上图所示,但是初看可能会有点懵,上面的表示是啥意思,好接下来总结下我的理解
最小二乘法(又称最小平方法)是一种数学优化技术,除了能拟合直线还能拟合曲线问题。
书中截取部分如果可以这样理解$$\alpha_{i}$$,如果是二次项的话$$y=\alpha_{1} x^{2}+\alpha_{2} x + \alpha_{3} $$,知道了吧,就是一个二项式子中的待解参数。
本文为了推导和笔记的简单化,直接以拟合直线 $$f(x;a,b): y=ax+b$$
[1]. 假设拟合直线 $$f(x;a,b): y=ax+b$$ [2]. 已经由n个样本$$(x_{n}, y_{n})$$ [3]. 误差$$e_{i}=y_{i}-(ax_{i}+b)$$ [4]. 当$$S = \sum_{i=1}^{n} e_{i}^{2}$$为最小值时,即得到的a,b参数就是最小二乘法得到的解. 如何求解这些参数(a,b)
∂ S ∂ b = − 2 ( ∑ i = 1 n y i − n b − a ∑ i = 1 n x i ) \frac{\partial S}{\partial b}=-2(\sum_{i=1}^{n}y_{i}-nb-a\sum_{i=1}^{n}x_{i}) ∂ b ∂ S = − 2 ( i = 1 ∑ n y i − n b − a i = 1 ∑ n x i )
∂ S ∂ a = − 2 ( ∑ i = 1 n x i y i − b ∑ i = 1 n x i − a ∑ i = 1 n x i 2 ) \frac{\partial S}{\partial a}=-2(\sum_{i=1}^{n}x_{i}y_{i}-b\sum_{i=1}{n}x_{i}-a\sum_{i=1}^{n}x_{i}^{2}) ∂ a ∂ S = − 2 ( i = 1 ∑ n x i y i − b i = 1 ∑ n x i − a i = 1 ∑ n x i 2 )
分别令上式中对a,b求偏导数的有点等于0,以此求取对a,b的最值.有:$$n\bar x=\sum_{i=1}^{n}x_i,n\bar y=\sum_{i=1}^{n}y_i$$
得到:
a = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 a=\frac {\sum_{i=1}^{n}({x_i-\bar x})(y_i-\bar y)} {\sum_{i=1}^{n}({x_i-\bar x})^2} a = ∑ i = 1 n ( x i − x ˉ ) 2 ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ )
b = y ˉ − a x ˉ b=\bar y-a\bar x b = y ˉ − a x ˉ
a = n ∑ x i y i − ∑ x i ∑ y i n ∑ x i 2 − ( ∑ x i ) 2 a=\frac {n\sum_{}^{}{x_iy_i}-\sum_{}^{}{x_i}\sum_{}^{}{y_i}} {n\sum_{}^{}{x_i}^2-(\sum_{}^{}{x_i})^2} a = n ∑ x i 2 − ( ∑ x i ) 2 n ∑ x i y i − ∑ x i ∑ y i
b = ∑ x i 2 ∑ y i − ∑ x i ∑ x i y i n ∑ x i 2 − ( ∑ x i ) 2 b=\frac {\sum_{}^{}{x_i}^2\sum_{}^{}{y_i}-\sum_{}^{}{x_i}\sum_{}^{}{x_iy_i}} {n\sum_{}^{}{x_i}^2-(\sum_{}^{}{x_i})^2} b = n ∑ x i 2 − ( ∑ x i ) 2 ∑ x i 2 ∑ y i − ∑ x i ∑ x i y i
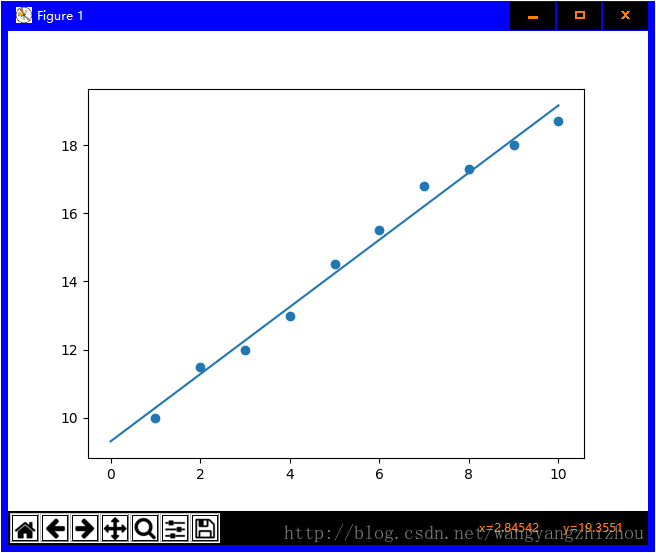
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 import numpy as npimport matplotlib.pyplot as pltdef calcAB (x,y ): n = len (x) sumX,sumY,sumXY,sumXX =0 ,0 ,0 ,0 for i in range (0 ,n): sumX += x[i] sumY += y[i] sumXX += x[i]*x[i] sumXY += x[i]*y[i] a = (n*sumXY -sumX*sumY)/(n*sumXX -sumX*sumX) b = (sumXX*sumY - sumX*sumXY)/(n*sumXX-sumX*sumX) return a,b, xi = [1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] yi = [10 ,11.5 ,12 ,13 ,14.5 ,15.5 ,16.8 ,17.3 ,18 ,18.7 ] a,b=calcAB(xi,yi) print ("y = %10.5fx + %10.5f" %(a,b))x = np.linspace(0 ,10 ) y = a * x + b plt.plot(x,y) plt.scatter(xi,yi) plt.show()
对于$$y=ax+b$$,转为向量的形式为
W = [ w 0 w 1 ] , X = [ 1 x 1 ] W=\begin{bmatrix} w_0\\ w_1 \end{bmatrix},X=\begin{bmatrix} 1\\ x_1 \end{bmatrix} W = [ w 0 w 1 ] , X = [ 1 x 1 ]
于是:
y = w 1 x 1 + w 0 = W T X y=w_1x_1+w_0=W^TX y = w 1 x 1 + w 0 = W T X
损失函数为:
L = 1 n ∑ i = 1 n ( y n − ( W T X ) 2 ) = 1 n ( y − X W ) T ( y − X W ) L=\frac{1}{n}\sum_{i=1}^{n}(y_n-(W^TX)^2)=\frac{1}{n}(y-XW)^T(y-XW) L = n 1 i = 1 ∑ n ( y n − ( W T X ) 2 ) = n 1 ( y − X W ) T ( y − X W )
最后可化为
1 n X T W T X W − 2 n X T W T y + 1 n y T y \frac{1}{n}X^TW^TXW-\frac{2}{n}X^TW^Ty+\frac{1}{n}y^Ty n 1 X T W T X W − n 2 X T W T y + n 1 y T y
令偏导为0
∂ L ∂ W = 2 n X T X W − 2 n X T y = 0 \frac{\partial L}{\partial W}=\frac{2}{n}X^TXW-\frac{2}{n}X^Ty=0 ∂ W ∂ L = n 2 X T X W − n 2 X T y = 0
另外:
(X^TX)^{-1}X^TX=E,EW=W$$,则 $$(X^TX)^{-1}X^TXW=(X^TX)^{-1}X^Ty,W=(X^TX)^{-1}X^Ty
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 import numpy as npimport matplotlib.pyplot as pltx = [1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] y = [10 ,11.5 ,12 ,13 ,14.5 ,15.5 ,16.8 ,17.3 ,18 ,18.7 ] A = np.vstack([x,np.ones(len (x))]).T a,b = np.linalg.lstsq(A,y)[0 ] print ("y = %10.5fx + %10.5f" %(a,b))x = np.array(x) y = np.array(y) plt.plot(x,y,'o' ,label='data' ,markersize=10 ) plt.plot(x,a*x+b,'r' ,label='line' ) plt.show()
拟合的效果(蓝线)
线性回归的目的是找到一个与这些数据最为温和的线性函数,用来预测或者分类,主要解决线性问题。
f ( x ) = ω 1 x 1 + ω 2 x 2 + ω 3 x 3 + . . . + ω d x d + b f(x)=\omega_{1}x_{1}+\omega_{2}x_{2}+\omega_{3}x_{3}+...+\omega_{d}x_{d}+b f ( x ) = ω 1 x 1 + ω 2 x 2 + ω 3 x 3 + . . . + ω d x d + b
一般向量形式写为:
f ( x ) = ω T x + b f(x)=\omega^{T}x+b f ( x ) = ω T x + b
其中的$$\omega=(\omega_{1};\omega_{2};\omega_{2};…\omega_{d})$$
x_{1},x_{2},...x_{k}$$是一组独立的预测变量 $$\omega_{1},\omega_{2},...\omega_{k}$$为模型从训练数据中学习得到的参数,或称赋予每个变量的权值。 b是一个学习到的参数,这个现行函数中的常量也称模型的偏置(Bias) * 根据输入属性可分为一元,二元......多元线性回归。 多元数据集的定义如下: $$D=\left [ x_{i,j}, y_{i}\right ]$$,其中i,表示数据集第i位序列的值,而j则表示在第i位x的属性是j种属性,即数据集中,x(i,j),i维行,j维纵坐标的矩阵。 即数据集j元的属性矩阵表示为:
\begin{bmatrix}
比如3元的表示一个西瓜好坏,【hue, root, echo】,加入预测函数的参数已经求得$$\omega=\left [ 0.2, 0.5, 0.3 \right ],b=1$$,则好瓜(good)函数$$f_{good}(x)=0.2 \cdot x_{hue}+0.5 \cdot x_{root}+0.3 \cdot x_{echo}+1
属性:
这里考虑一元的情况则数据集为: $$D=\left [ x_{i}, y_{i}\right ]_{i=1}^{m} $$,即上面矩阵表示的j元数据集中j=1,现在我们来尝试一元的线性回归。
[1] 假设我们预测函数形式:$$f(x_{i})=\omega x_{i}+b_{i}$$,使得$$f(x_{i})\approx y_{i}$$. 接下来我们引入上面的最小二乘法求参数$$\omega , b$$.
e ω ∗ , b ∗ = a r g ( ω , b ) m i n ∑ i = 1 m ( f ( x i ) − y i ) 2 e_{\omega^*,b^*}=arg_{(\omega,b)}min \sum_{i=1}^{m}(f(x_{i})-y_{i})^2 e ω ∗ , b ∗ = a r g ( ω , b ) m i n i = 1 ∑ m ( f ( x i ) − y i ) 2
∂ E ω , b ∂ ω = 2 ( ω ∑ i = 1 m x i 2 − ∑ i = 1 m ( y i − b ) x i ) \frac{\partial E_{\omega,b}}{\partial \omega}=2(\omega\sum_{i=1}^{m}x_{i}^{2}-\sum_{i=1}^{m}(y_{i}-b)x_{i}) ∂ ω ∂ E ω , b = 2 ( ω i = 1 ∑ m x i 2 − i = 1 ∑ m ( y i − b ) x i )
∂ E ω , b ∂ b = 2 ( m b − ∑ i = 1 m ( y i − ω x i ) ) \frac{\partial E_{\omega,b}}{\partial b}=2(mb-\sum_{i=1}^{m}(y_{i} - \omega x_{i})) ∂ b ∂ E ω , b = 2 ( m b − i = 1 ∑ m ( y i − ω x i ) )
[5] 上一步骤中的偏导数都设为零,以此来求得$$\omega , b$$. ω = ∑ i = 1 m y i ( x i − x ˉ ) ∑ i = 1 m x i 2 − 1 m ( ∑ i = 1 m x i ) 2 \omega = \frac{\sum_{i=1}^{m} y_{i}(x_{i}-\bar{x})}{\sum_{i=1}^{m}x_{i}^{2}-\frac{1}{m}(\sum_{i=1}^{m}x_{i})^2} ω = ∑ i = 1 m x i 2 − m 1 ( ∑ i = 1 m x i ) 2 ∑ i = 1 m y i ( x i − x ˉ )
b=\frac{1}{m}\sum_{i=1}^{m}(y_{i}-\omega x_{i}),\bar{x}=\frac{1}{m}\sum_{i=1}^{m}x_{i}$$,$$\bar{x}$$为序列x的均值。 > 这里一元的线性回归,用最小二乘法求解的参数估计,称为线性回归模型的最小二乘法“参数估计”(parameter estimation). ## 2.2 多元线性回归 类似一元,但是求解 估计的参数矩阵$$\omega, b$$,就需要全部看成矩阵的求解方法求出。见最小二乘法矩阵推导那一节,不再具体推推导了,在2.1节基础上明白线性回归,多元回归思想即可明白。